Comparing ivis with other dimensionality reduction algorithms

Ivis aims to reduce data dimensionality whilst preserving both global and local structures. There are a number of real-world applications where this feature could be useful. For example:

• Anomaly detection
• Biological interpretation of high-throughput experiments
• Feature extraction

Several algorithms have been proposed to address the problem of dimensionality reduction, including UMAP and t-SNE. UMAP in particular, has been succesfully applied in machine learning pipelines. Ivis is different to these approaches in several ways.

First, ivis does not make any assumptions as to the inherent structure of the dataset. Second, ivis is designed to handle both small and extremely large datasets. Ivis performs well on toy datasets such as the iris dataset, and scales linearly to datasets with millions of observations. Indeed, we see that the main usecase for ivis are datasets with > 250,000 observations. Finally, ivis prioritises interpretation over visual apperance - this is accomplished by imposing meaning to distances between points in the embedding space. As such, ivis does not create spurious clusters nor does it artificially pack clusters closer together. Embeddings aim to be true to the original structure of the data, which can be noisy in a real-world setting.

Visual Assessment

We will visually examine how popular dimensionality reduction algorithms - UMAP, t-SNE, Isomap, MDS, and PCA - approach two synthetic datasets with 5,000 observations in each. Since we are concerned with a dimensionality reduction problem, we will artificially add reduntant features to the original datasets using polynomial combinations (degree ≤ 10) of the original features.

Random Noise

To start, let’s examine how various dimensionality reduction methods behave in the presence of random noise. We generated 5000 uniformly distributed random points in a two-dimensional space and expanded the feature set using polynomial combinations. In all cases default parameters were used to fit multiple models.

Both ivis and PCA reliably recovered the random nature of our dataset. Conversely, Isomap, UMAP, and t-SNE appeared to pack certain points together, creating an impression of clusters within uniform random noise.

Structured Datasets

Next, we examine how well global features of a dataset, such as relative position of clusters, can be recovered in a low-dimensional space.

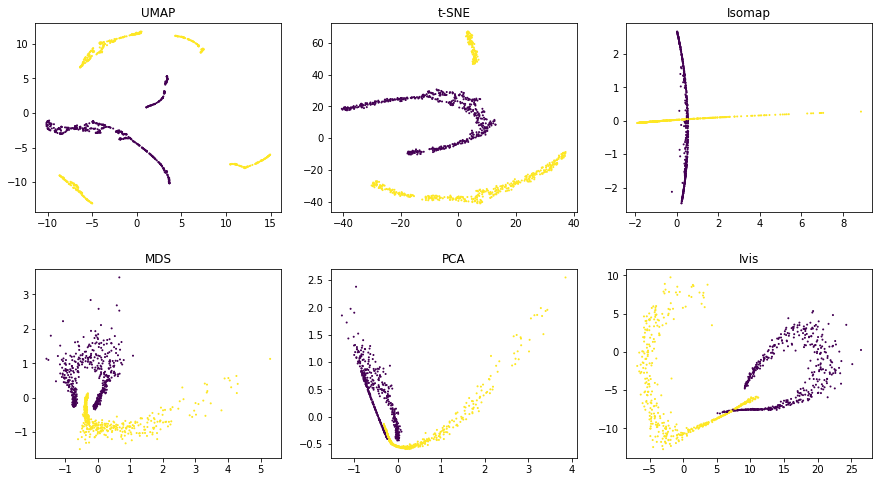
Using default parameters, we can see that ivis captures both the general structure of each half-moon, as well as their relative positions to one another. Both UMAP and t-SNE appear to introduce spurious clusters and global relationships between the half-moons appear to be disrupted.

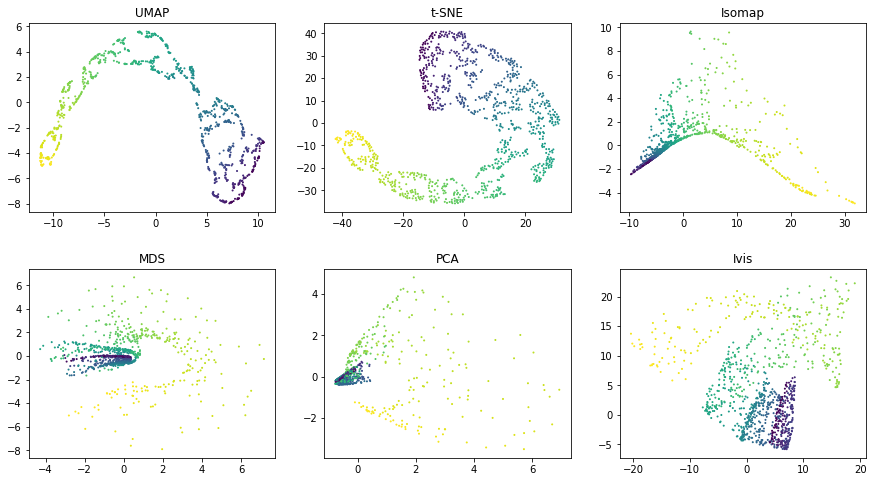
Similarly as above, UMAP and t-SNE appear to generate a large number of small clusters along the continuous distribution of the dataset. Although the global structure is relatively well-preserved. ivis maintains both global and local structures of the dataset.

Quantitative Evaluation

To measure how well each algorithm preserves global distances, we examined correlation between points in the original dataset and the embedding space. For this analysis, 10,000 observations were chosen from the Levine dataset (104,184 x 32) using random uniform sampling. Box plots represent distances across pairs of points in the embeddings, binned using 50 equal-width bins over the pairwise distances in the original space. Pearson correlation coefficients were also computed over the pairs of distances.

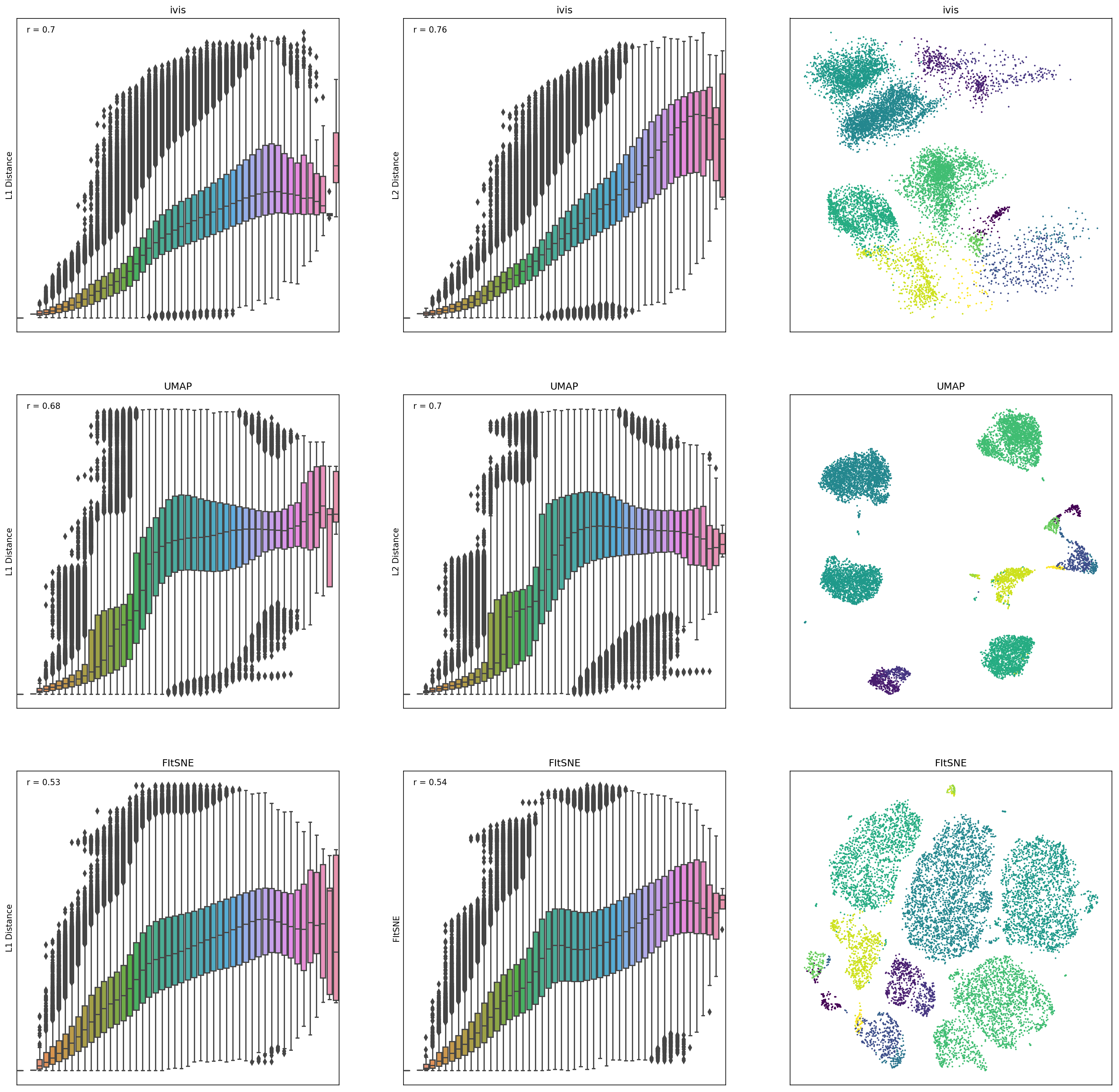
ivis appeared to preserve both a small-, mid-, and large-scale L1 and L2 distances, whilst UMAP and t-SNE seemed to ignore mid- to large-scale distances. Interestingly, ivis was particularly good at preserving L2 distances in low-dimensional space.